监督学习之树模型（2）

决策树算法的基本思想是以信息熵为度量构造一棵值下降最快的树。因此需要理解如下几个概念。

熵

为了理解熵，必须讲一点物理学。热力学第二定律表达了有很多种解释，有一种最容易懂：能量转换的时候，大部分能量会转换成预先设定的状态，比如热能变成机械能、电能变成光能。但是，还有一部分能量会生成新的状态。
状态多，就是可能性多，表示比较混乱；状态少，就是可能性少，相对来说就比较有秩序。因此，能量转换会让系统的混乱度增加，熵就是系统的混乱度。
“熵”是一种无序程度的量度，意思是越混乱越无规律熵值就越大，反之熵值越小。

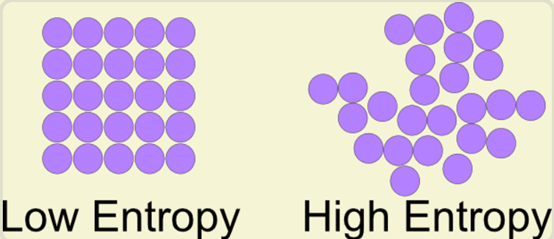
熵让我们理解了一件事，如果不施加外力影响，事物永远向着更混乱的状态发展。

信息熵

假设我们要做一个游戏，每次从盒子中抽一个小球记录颜色后放回，如果抽4次的结果和盒子中球的分布一致的话我们获胜，这三种不同组合中第一个盒子最容易获胜，第二个次之，第三个获胜概率最低。

第一个盒子：1x1x1x1=1
第二个盒子：0.75x0.75x0.75x0.25=0.105
第三个盒子：0.5x0.5x0.5x0.5=0.0625
因为和比积好，接下来我们把这个公式变形。

log2(ab) = log2(a) + log2(b)

根据上面的公式，第二个盒子的获胜概率可以换一种形式表示

0.75x0.75x0.75x0.25 = 0.105
log2(0.75)+log2(0.75)+log2(0.75)+log2(0.25) = -3.245

那么获胜几率可以转换成如下的表格。

接着增大球的数量，有如下公式

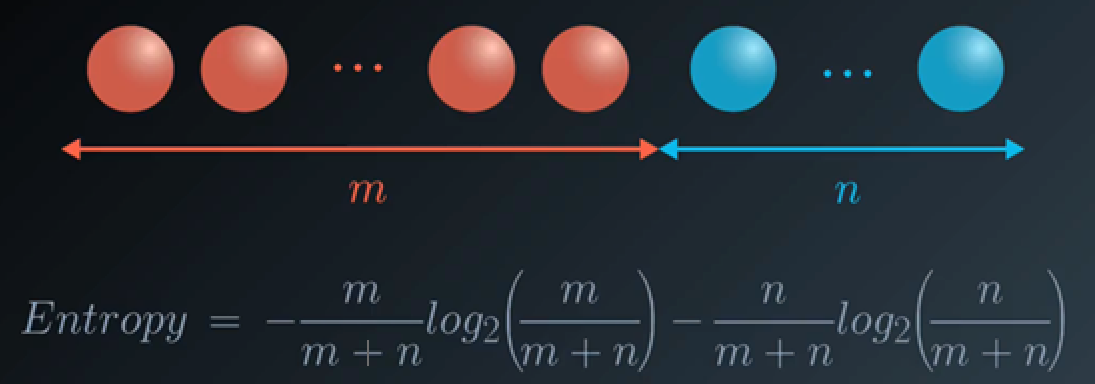
这就是1948年香农提出的信息熵（Entropy）的概念。
假如事件A的分类划分是（A₁,A₂,…,A_n），每部分发生的概率是(p₁,p₂,…,p_n)，那信息熵定义为公式如下：

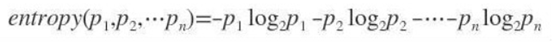
信息增益

信息增益又称相对熵（relative entropy），是针对一个一个的特征而言的，就是看一个特征X，系统有它和没它的时候信息量各是多少，两者的差值就是这个特征给系统带来的信息增益。
信息增益的公式很简单，就是信息熵的变化。

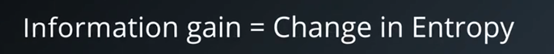
当两个子节点大小一致时，就是父节点的熵减去子节点熵的平均值。

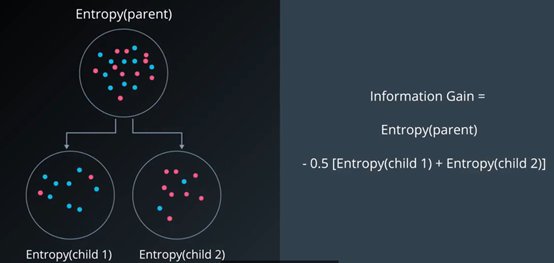
我们可以通过下面的例子来进行理解：

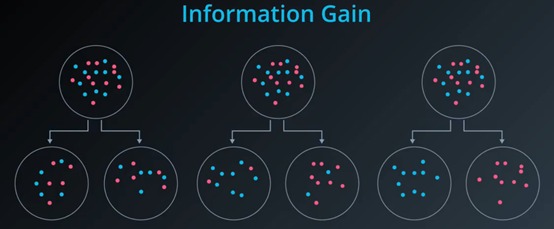
问题：假设每个子集大小一样都是10个点，哪种分法的效果最好？

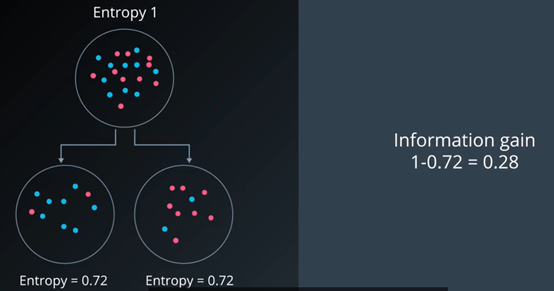
第一种分法，能提供的信息变化较少。

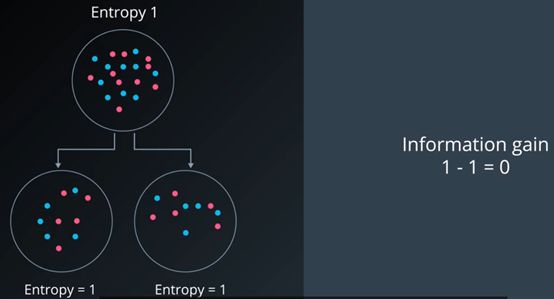
第二种分法很糟糕，没有提供任何信息增益。

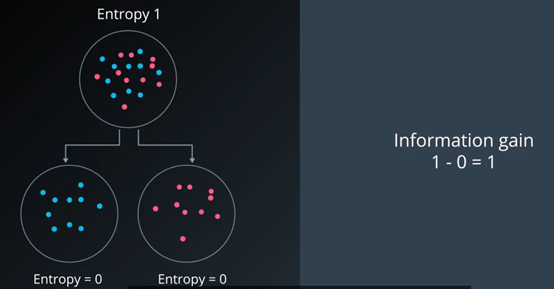
第三种分法很好，完美地分割了数据。

如果两个子节点的大小不一样该怎么办？这就引出了条件熵的概念。

$$条件熵 = \sum_{i=1}^n(\frac{子数据集大小}{数据集大小}*子数据集的信息熵)$$

结合条件熵的概念，我们把信息增益的公式写为

$$信息增益 = 父节点的信息熵-子节点的条件熵$$