图算法之最小生成树

发表于 更新于
将给出的所有点连接起来且连接路径之和最小的图叫最小生成树。要解决最小生成树问题，通常采用两种算法：Prim算法和Kruskal算法。

将给出的所有点连接起来（即从一个点可到任意一个点）且连接路径之和最小的图叫最小生成树。要解决最小生成树问题，通常采用两种算法：Prim算法和Kruskal算法。
一般来说，prim算法适合稠密图，kruskal算法适合稀疏图。

Prim算法

Prim算法构建最小生成树的过程是：先构建一棵只包含顶点V1的树A，然后每次在连接树A顶点和图G中树A以外的顶点的所有边中，选取一条权重最小的边加入树A，直至树A覆盖图G中的所有顶点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def MiniSpanTree_prim(nodes, graph):
    wsum = 0
    Spantree = []  # 最小生成树
    Selected = []   # 已选择节点
    Candidate = []  # 未选择节点

    n = len(nodes)
    for i in range(n):
        Candidate.append(i)  # 一开始所有顶点都在Candidate中

    Selected.append(0)   # 将根节点移入Selected
    Candidate.remove(0)   # 将根节点移出Candidate
    
    while len(Candidate)>0:
        [begin, end, minweight] = [-1, -1, 9999]
        for i in Selected:
            for j in Candidate:
                if graph[i][j] < minweight:  
                    minweight = graph[i][j]
                    begin = i
                    end = j
        Spantree.append([begin, end, minweight])
        wsum += minweight
        Selected.append(end)
        Candidate.remove(end)

    print("最小生成树总权值:"+str(wsum))
    print("最小生成树:", Spantree)
    print("插入顶点顺序："+str(Selected))

if __name__=='__main__':
    nodes = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']

    MAX = 9999
    matrix = [[MAX,  10, MAX, MAX, MAX,  11, MAX, MAX, MAX],
              [10,  MAX,  18, MAX, MAX, MAX,  16, MAX,  12],
              [MAX,  18, MAX,  22, MAX, MAX, MAX, MAX,   8],
              [MAX, MAX,  22, MAX,  20, MAX, MAX,  16,  21],
              [MAX, MAX, MAX,  20, MAX,  26,   7,  19, MAX],
              [11,  MAX, MAX, MAX,  26, MAX,  17, MAX, MAX],
              [MAX,  16, MAX, MAX,   7,  17, MAX,  19, MAX],
              [MAX, MAX, MAX,  16,  19, MAX,  19, MAX, MAX],
              [MAX,  12,   8,  21, MAX, MAX, MAX, MAX, MAX]]

    MiniSpanTree_prim(nodes, matrix)

Kruskal算法

Kruskal算法构建最小生成树的过程是：令树T的初始状态为|V|个结点而无边的非连通图，树T中的每个顶点自成一个连通分量。接着，每次从图G中所有两个端点落在不同连通分量的边中，选取权重最小的那条，将该边加入树T中，如此往复，直至树T中所有顶点都在同一个连通分量上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def MiniSpanTree_kruskal(nodes, graph):
    n = len(nodes)
    # 整理出当前树的边集
    edges = []
    for i in range(n):
        for j in range(n - i):
            weight = graph[i][i+j]
            if weight < 9999:   # 鉴定是否有边
                edges.append([i, i+j, weight])
    edges.sort(key=lambda x:x[2])  # 对边集中的边排序

    wsum = 0
    Spantree = []  # 最小生成树
    trees = [[i] for i in range(n)]  # 所有树的集合
    for edge in edges:
        tree1 = edge[0]               
        tree2 = edge[1]
        for i in range(len(trees)):
            if tree1 in trees[i]:
                tree1 = i
            if tree2 in trees[i]:
                tree2 = i
        if tree1 != tree2:    # 若两顶点不在同一棵树上，链接两顶点
            Spantree.append(edge)
            wsum += edge[2]
            trees[tree1] = trees[tree1] + trees[tree2]
            trees[tree2] = []

    print("最小生成树总权值:"+str(wsum))
    print("最小生成树:", Spantree)

if __name__=='__main__':
    nodes = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']

    MAX = 9999
    matrix = [[MAX,  10, MAX, MAX, MAX,  11, MAX, MAX, MAX],
              [10,  MAX,  18, MAX, MAX, MAX,  16, MAX,  12],
              [MAX,  18, MAX,  22, MAX, MAX, MAX, MAX,   8],
              [MAX, MAX,  22, MAX,  20, MAX, MAX,  16,  21],
              [MAX, MAX, MAX,  20, MAX,  26,   7,  19, MAX],
              [11,  MAX, MAX, MAX,  26, MAX,  17, MAX, MAX],
              [MAX,  16, MAX, MAX,   7,  17, MAX,  19, MAX],
              [MAX, MAX, MAX,  16,  19, MAX,  19, MAX, MAX],
              [MAX,  12,   8,  21, MAX, MAX, MAX, MAX, MAX]]

    MiniSpanTree_kruskal(nodes, matrix)

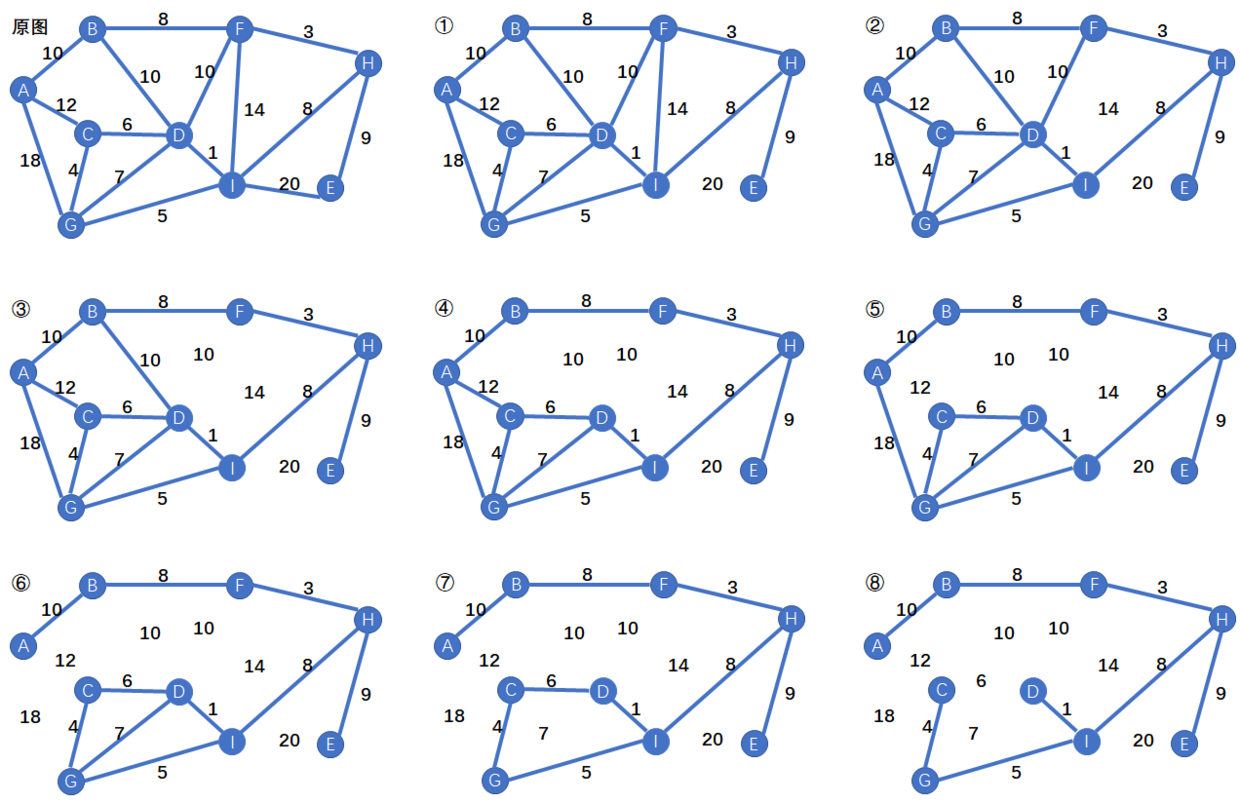
破圈法

这种方法最早是管梅谷教授在1974年提出来的，这种方法很巧妙，也很好玩，就是这个连通图肯定是连通的嘛，那环肯定是有的，那我就把你的环给破坏了，而且挑权重最大的那条边来破坏，不停地破下去，直到所有的顶点都处于同一个连通分量上，并且边数为n-1条。