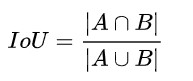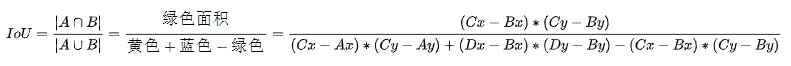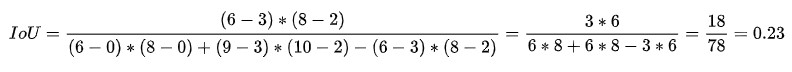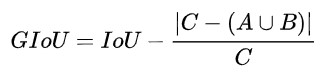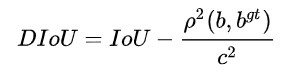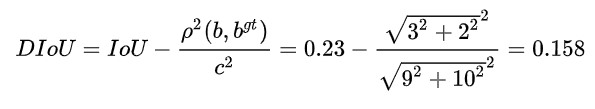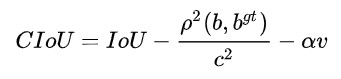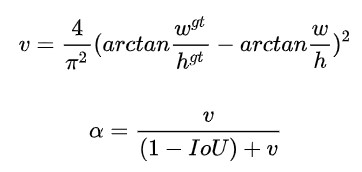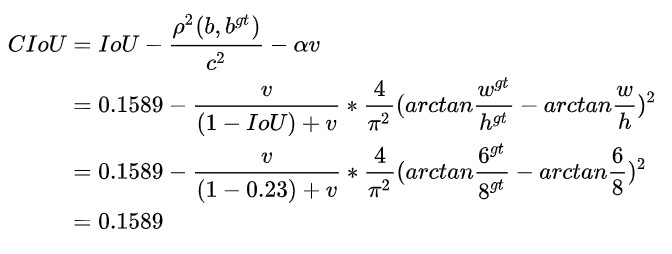目标检测基础模块之IoU及其改进

发表于 更新于
IoU又名交并比，是一种计算不同图像相互重叠比例的算法，时常被用于深度学习领域的目标检测或语义分割任务中。

一、IoU简介

IoU又名交并比，是一种计算不同图像相互重叠比例的算法，时常被用于深度学习领域的目标检测或语义分割任务中。

1、在目标检测中的应用

2、在语义分割中的应用

二、IoU原理

1、定义

IoU的定义如下：

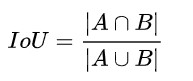
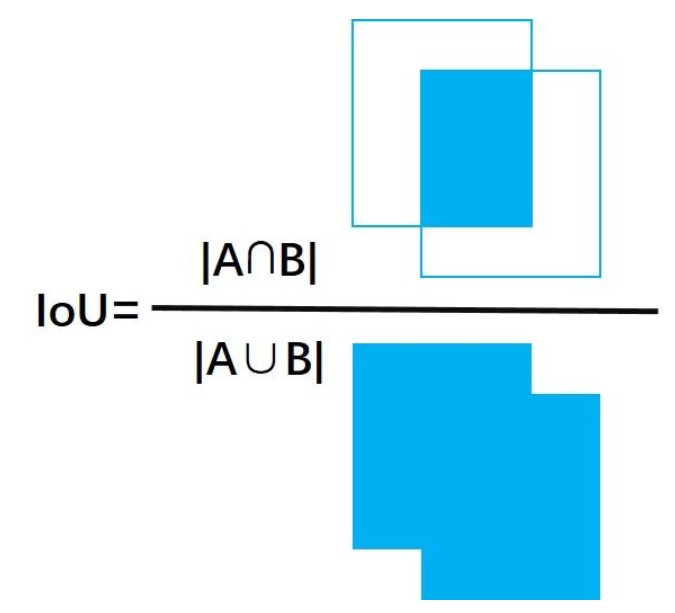
直观来讲，我们可以把IoU的值定为为两个图形面积的交集和并集的比值。

2、计算

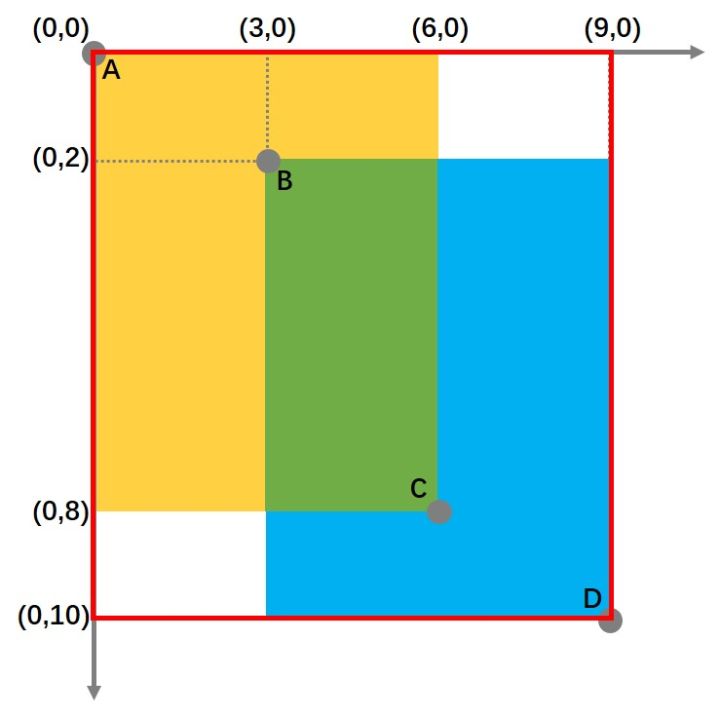
如上图所示，黄色矩形与蓝色矩形相交，他们的顶点A、B、C、D分别是(0,0)、(3,2)、(6,8)、(9,10)
此时IoU的计算公式应为：

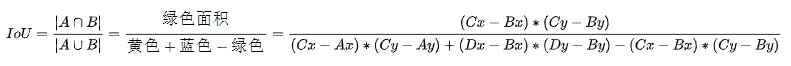
带入A、B、C、D四点的实际坐标后，可以得到：

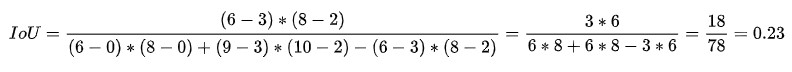
三、IoU的代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def IoU(boxA, boxB):

    # 计算相交区域的宽高
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])

    # 计算交集、并集面积
    interArea = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    unionArea = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
                (box2[2] - box2[0]) * (box2[3] - box2[1]) - interArea

    # 计算IOU
    IoU = interArea/unionArea

    return IoU

# box:[上左, 下右]
box1 = [0, 0, 8, 6]
box2 = [2, 3, 10, 9]

print(IoU(box1, box2))

四、IoU的改进

1、GIoU

GIoU（Generalized Intersection over Union）相较于IoU多了一个”Generalized”，这也意味着它能在更广义的层面上计算IoU，并解决”两个图像没有相交时，无法比较两个图像的距离远近”的问题。
GIoU的计算公式为：

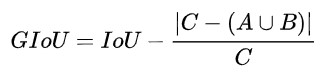
其中C代表两个图像的最小包庇面积，也可以理解为这两个图像的最小外接矩形的面积。

计算GIoU：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def GIoU(boxA, boxB):

    # 计算最小包庇面积
    cArea = (max(boxA[0], boxA[2], boxB[0], boxB[2]) - min(boxA[0], boxA[2], boxB[0], boxB[2])) * \
            (max(boxA[1], boxA[3], boxB[1], boxB[3]) - min(boxA[1], boxA[3], boxB[1], boxB[3]))

    # 计算相交区域的宽高
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])

    # 计算交集、并集面积
    interArea = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    unionArea = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
                (box2[2] - box2[0]) * (box2[3] - box2[1]) - interArea

    # 计算IOU
    IoU = interArea/unionArea

    # 计算空白部分占比
    endArea = (cArea - unionArea)/cArea
    GIoU = IoU - endArea

    return GIoU

# box:[上左, 下右]
box1 = [0, 0, 8, 6]
box2 = [2, 3, 10, 9]

print(GIoU(box1, box2))

2、DIoU

GIoU虽然解决了IoU的一些问题，但是它并不能直接反映预测框与目标框之间的距离，DIoU（Distance-IoU）解决了这一问题，它将两个框之间的重叠度、距离、尺度都考虑了进来。
DIoU的计算公式如下：

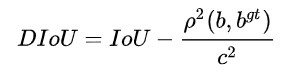
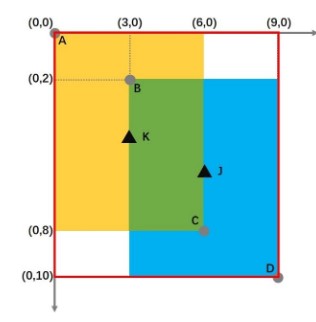
通过计算可得，黄框中心点K、蓝框中心点J的坐标分别为(3,4)、(6,6)
计算DIoU：

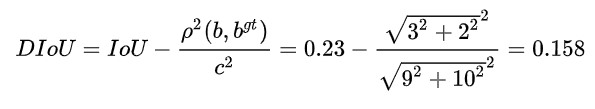
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import numpy as np

def IoU(boxA, boxB):

    # 计算相交区域的宽高
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])

    # 计算交集、并集面积
    interArea = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    unionArea = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
                (box2[2] - box2[0]) * (box2[3] - box2[1]) - interArea

    # 计算IOU
    IoU = interArea/unionArea

    return IoU

def DIoU(boxA, boxB):

    # 计算对角线长度
    c = np.sqrt((max(boxA[0], boxA[2], boxB[0], boxB[2]) - min(boxA[0], boxA[2], boxB[0], boxB[2]))**2 + \
                (max(boxA[1], boxA[3], boxB[1], boxB[3]) - min(boxA[1], boxA[3], boxB[1], boxB[3]))**2)

    # 计算中心点间距
    point_1 = ((boxA[0] + boxA[2])/2, (boxA[1] + boxA[3])/2)
    point_2 = ((boxB[0] + boxB[2])/2, (boxB[1] + boxB[3])/2)
    d = np.sqrt((point_2[0] - point_1[0])**2 + (point_2[1] - point_1[1])**2)

    # 计算IOU
    iou = IoU(boxA, boxB)

    # 计算空白部分占比
    lens = d**2 / c**2
    diou = iou - lens

    return diou

# box:[上左, 下右]
box1 = [0, 0, 8, 6]
box2 = [2, 3, 10, 9]

print(DIoU(box1, box2))

3、CIoU

CIoU的全称为Complete IoU，它在DIoU的基础上，还能同时考虑两个矩形的长宽比，也就是形状的相似性。
CIoU的计算公式如下：

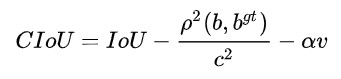
其中α是权重函数，而v用来度量长宽比的相似性：

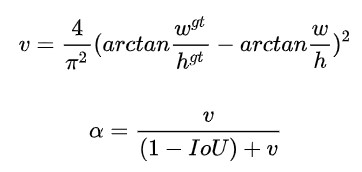
可以看出，CIoU就是在DIoU的基础上，增加了图像相似性的影响因子，因此可以更好的反映两个框之间的差异性。

通过计算可得，黄框中心点K、蓝框中心点J的坐标分别为(3,4)、(6,6)
计算CIoU：

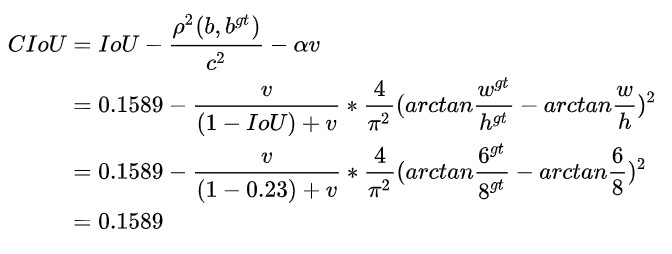
两个形状差别越大，CIoU相较于DIoU则越小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import math

def IoU(boxA, boxB):
    # 计算相交区域的宽高
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])

    # 计算交集、并集面积
    interArea = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    unionArea = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
                (box2[2] - box2[0]) * (box2[3] - box2[1]) - interArea

    # 计算IOU
    IoU = interArea/unionArea
    return IoU

def DIoU(boxA, boxB):
    # 计算对角线长度
    c = np.sqrt((max(boxA[0], boxA[2], boxB[0], boxB[2]) - min(boxA[0], boxA[2], boxB[0], boxB[2]))**2 + \
                (max(boxA[1], boxA[3], boxB[1], boxB[3]) - min(boxA[1], boxA[3], boxB[1], boxB[3]))**2)

    # 计算中心点间距
    point_1 = ((boxA[0] + boxA[2])/2, (boxA[1] + boxA[3])/2)
    point_2 = ((boxB[0] + boxB[2])/2, (boxB[1] + boxB[3])/2)
    d = np.sqrt((point_2[0] - point_1[0])**2 + (point_2[1] - point_1[1])**2)

    # 计算IOU
    iou = IoU(boxA, boxB)

    # 计算空白部分占比
    lens = d**2 / c**2
    diou = iou - lens
    return diou

def CIoU(boxA, boxB):

    iou = IoU(box1, box2)
    diou = DIoU(box1, box2)

    v = 4/math.pi**2 * (math.atan((boxA[2] - boxA[0])/(boxA[3] - boxA[1])) - math.atan((boxB[2] - boxB[0])/(boxB[3] - boxB[1])))**2
    alpha = v / (1-iou) + v

    ciou = diou - alpha * v

    return ciou

# box:[上左, 下右]
box1 = [0, 0, 8, 6]
box2 = [2, 3, 10, 9]

print(CIoU(box1, box2))