图算法之遍历

两种图的遍历算法：广度优先（BFS）与深度优先（DFS）。
广度优先遍历的路径通常短而直接，深度优先遍历的路径通常长而曲折。

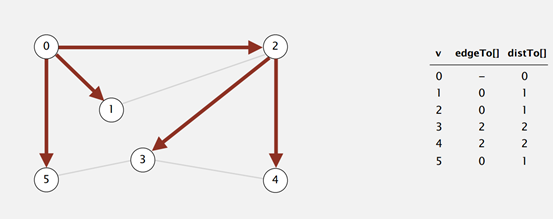
广度优先遍历

从起点开始，遍历所有与起点连通的顶点，再遍历与这些顶点连通的顶点，即先搜索距离起点距离为1的顶点，再遍历与起点距离为2的顶点…..

def bfsTravel(graph, source):
    '''
    广度优先遍历
    INPUT -> 用邻接表存储的图, 开始遍历的源节点
    '''
    frontiers = [source]     # 表示前驱节点
    travel = [source]       # 表示遍历过的节点
    # 当前驱节点为空时停止遍历
    while frontiers:        
        nexts = []          # 当前层的节点（相比frontier是下一层）
        for frontier in frontiers:
            for current in graph[frontier]: # 遍历当前层的节点(体现广度)
                if current not in travel:   # 判断是否访问过
                    travel.append(current)  # 没有访问过则入队
                    nexts.append(current)   # 当前结点作为前驱节点
        frontiers = nexts   # 更改前驱节点列表
    return travel

if __name__ == '__main__':

    Graph = {'A':  ['B', 'C', 'D'],
             'B':  ['E'],
             'C':  ['D', 'F'],
             'D':  ['B', 'E', 'G'],
             'E':  [],
             'F':  ['D', 'G'],
             'G':  ['E']}
    
    r = bfsTravel(Graph, 'A')        # 搜索A到D的所有路径
    print(r)

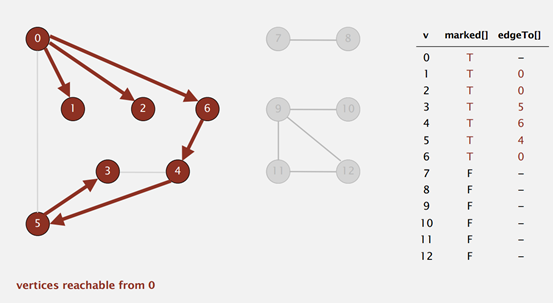
深度优先遍历

从起点开始选择一条边走到下一个顶点，每到一个顶点便标记此顶点已到达，当来到一个标记过的顶点时回退到上一个顶点，再选择一条没有到达过的顶点……直到所有顶点都被访问。

def dfsTravel(graph, source):
    '''
    深度优先遍历
    INPUT -> 用邻接表存储的图, 开始遍历的源节点
    '''
    travel = []     # 存放访问过的节点的列表
    stack = [source]      # 构造一个堆栈
    while stack:            # 堆栈空时结束    
        current = stack.pop()       # 堆顶出队
        if current not in travel:   # 判断当前结点是否被访问过
            travel.append(current)  # 如果没有访问过，则将其加入访问列表
        for next_adj in graph[current]: # 遍历当前结点的下一级
            if next_adj not in travel:  # 没有访问过的全部入栈
                stack.append(next_adj)
    return travel

if __name__ == '__main__':

    Graph = {'A':  ['B', 'C', 'D'],
             'B':  ['E'],
             'C':  ['D', 'F'],
             'D':  ['B', 'E', 'G'],
             'E':  [],
             'F':  ['D', 'G'],
             'G':  ['E']}
    
    r = dfsTravel(Graph, 'A')        # 搜索A到D的所有路径
    print(r)