用networkx解决图论问题（1）

设备更新问题

例：某种工程设备的役龄为4年，每年年初都面临着是否更新的问题：若卖旧买新，就要支付一定的购置费用；若继续使用，则要支付更多的维护费用，且使用年限越长维护费用越多。若役龄期内每年的年初购置价格、当年维护费用及年末剩余净值如下表所示。

年份	1	2	3	4
年初购置费用/万元	25	26	28	31
当年维护费用/万元	10	14	18	26
年末剩余净值/万元	20	16	13	11

请为该设备制订一个4年役龄期内的更新计划，使总的支付费用最少。
解：可以把这个问题化为图论中的最短路径问题。
构造赋权有向图D = (V,A,W)，其中顶点集V = {v₁,v₂,…,v₅}，这里v_i(i=1,2,3,4)表示第i年年初的时刻，v₅表示第4年年末的时刻，A为弧的集合，邻接矩阵W = (w_ij)_5X5，这里w_ij为第i年年初至第j年年初（或j-1年年末）期间所支付的费用，计算公式为

$w_{ij}=p_{i}+\sum\limits_{k=1}^{j-i}a_{k}-r_{j-i} $

其中p_i为第i年年初的购置价格，a_k为第k年当年的维护费用，r_i为已使用i年的旧设备的出售价格(残值)。则邻接矩阵为

$ W = \begin{bmatrix} 0 & 15 & 33 & 54 & 82 \\ \infty & 0 & 16 & 34 & 55 \\ \infty & \infty & 0 & 18 & 36 \\ \infty & \infty & \infty & 0 & 21 \\ \infty & \infty & \infty & \infty & 0 \end{bmatrix} $

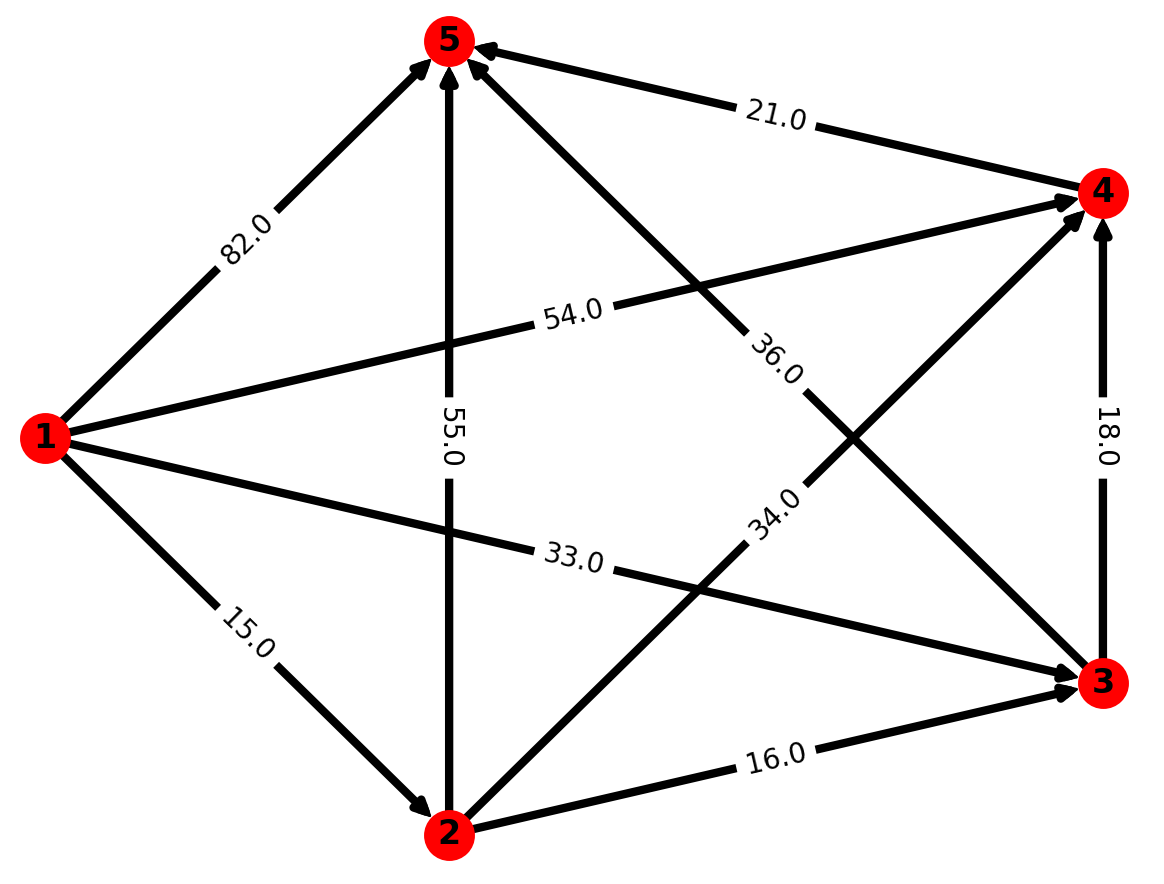
那么制订总的支付费用最小的设备更新计划，就是在下图所示的有向图D中寻找顶点v₁到顶点v₅的费用最短路径。

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

p = [25, 26, 28, 31]  # 购置价格
a = [10, 14, 18, 26]  # 维护费用
r = [20, 16, 13, 11]  # 售出残值

w = np.zeros((5, 5))  # 权值矩阵初始化
for i in range(5):
    for j in range(i+1, 5):
        w[i, j] = p[i] + np.sum(a[0:j-i]) - r[j-i-1]
print(w)

G = nx.DiGraph(w)
p = nx.dijkstra_path(G, source=0, target=4, weight='weight')
print('最短路径是', np.array(p)+1)

d = nx.dijkstra_path_length(G, source=0, target=4, weight='weight')
print('最短距离是', d)

s = dict(zip(range(5), range(1,6)))
pos = nx.shell_layout(G)  # 设置布局
G_w = nx.get_edge_attributes(G, 'weight')
nx.draw(G, pos, font_weight='bold', labels=s, node_color='r')
nx.draw_networkx_edge_labels(G, pos, edge_labels=G_w)
nx.draw_networkx_edges(G, pos, width=3)
plt.show()