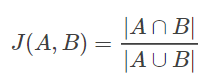相似性度量,即综合评定两个事物之间相近程度的一种度量。两个事物越接近,它们的相似性度量也就越大,而两个事物越疏远,它们的相似性度量也就越小。相似性度量的给法种类繁多,一般根据实际问题进行选用。
绝对值/曼哈顿距离
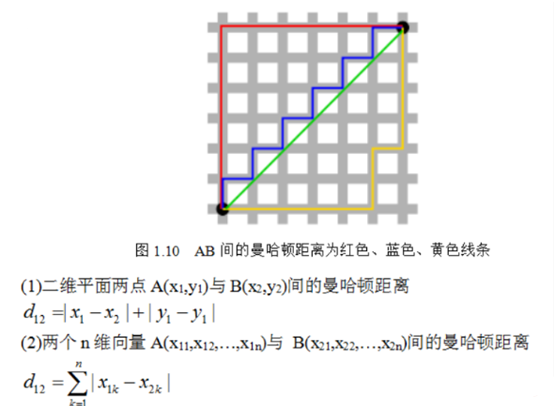
从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”(L1范数)。而这也是曼哈顿距离名称的来源,曼哈顿距离也称为城市街区距离(City Block distance)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| import numpy as np
def manhattan_dist(p, q):
'''
曼哈顿距离/绝对距离
INPUT -> 长度一致的向量1、向量2
举例: p = [1,2,6]; q = [1,3,5]
'''
p = np.mat(p)
q = np.mat(q)
return np.sum(np.abs(p-q))
p = [1,3,2,3,4,3]
q = [1,3,4,3,2,3]
print(manhattan_dist(p,q))
|
欧氏距离
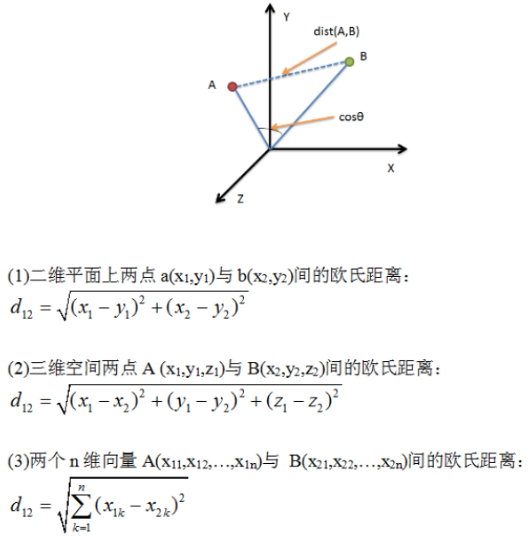
欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| import numpy as np
import math
def euclidean_dist(p, q):
'''
欧氏距离
INPUT -> 长度一致的向量1、向量2
'''
p = np.mat(p)
q = np.mat(q)
return math.sqrt(np.sum(np.power(p-q, 2)))
def euclidean_dist_2(p, q):
'''
坐标点间欧氏距离(速度快)
INPUT -> 坐标1、坐标2
'''
return math.sqrt(math.pow(p[0]-q[0], 2)+math.pow(p[1]-q[1], 2))
def standardized_euclidean_dist(p, q):
'''
标准化欧氏距离
INPUT -> 长度一致的向量1、向量2
'''
sumnum = 0
for i in range(len(p)):
avg = (p[i]-q[i])/2
si = math.sqrt((p[i]-avg)**2+(q[i]-avg)**2)
sumnum += ((p[i]-q[i])/si )**2
return math.sqrt(sumnum)
|
切比雪夫距离
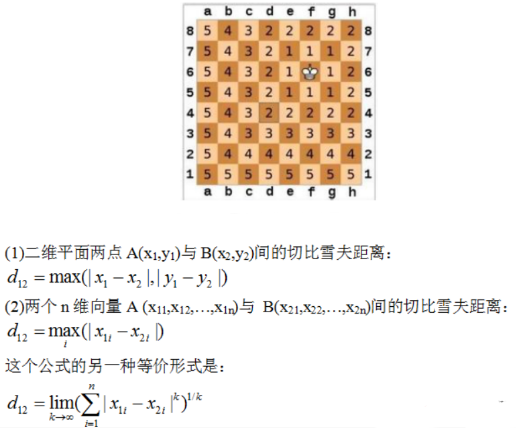
国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的任意一个(如下图)。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?自己走走试试。你会发现最少步数总是max(|x2-x1| , |y2-y1|) 步。有一种类似的一种距离度量方法叫切比雪夫距离。
1
2
3
4
5
6
7
8
9
10
11
12
| import numpy as np
def chebyshev_dist(p, q):
'''
切比雪夫距离
INPUT -> 长度一致的向量1、向量2
'''
p = np.mat(p)
q = np.mat(q)
return np.max(np.abs(p-q))
|
编辑距离和汉明距离
编辑距离,又称Levenshtein距离,是指两个字符串之间由一个转成另一个所需的最少编辑操作次数。例如,”101”与”1111”之间的编辑距离是2。
汉明距离,是两个等长字符串(编辑距离没这个要求)之间对应位置的不同字符的个数。例如,”1011101”与”1001001”之间的汉明距离是2。
编辑距离只考虑是一个字符串转化为另外一个的最快速度,不考虑不同位的含义。而汉明距离更多的是强调向量,即每一位的值都有相应的实际意义,不会交换位置。比如说,有两个对象A=”909”,B=”090”。A与B的编辑距离ED(A, B)=2,汉明距离H(A, B)=3。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| import Levenshtein
import numpy as np
s1 = '909'
s2 = '090'
print(Levenshtein.distance(s1, s2))
print(Levenshtein.hamming(s1, s2))
def edit_dist(word1, word2):
len1 = len(word1)
len2 = len(word2)
dp = np.zeros((len1 + 1, len2 + 1))
for i in range(len1 + 1):
dp[i][0] = i
for j in range(len2 + 1):
dp[0][j] = j
for i in range(1, len1 + 1):
for j in range(1, len2 + 1):
delta = 0 if word1[i-1] == word2[j-1] else 1
dp[i][j] = min(dp[i - 1][j - 1] + delta, min(dp[i-1][j] + 1, dp[i][j - 1] + 1))
return int(dp[len1][len2])
def hamming_dist(word1, word2):
diffs = 0
if len(word1) != len(word2):
return 'it is wrong!'
for ch1, ch2 in zip(word1, word2):
if ch1 != ch2:
diffs += 1
return diffs
print(edit_dist(s1, s2))
print(hamming_dist(s1, s2))
def hamming_dist2(p, q):
p = np.mat(p)
q = np.mat(q)
smstr = np.nonzero(p-q)
return np.shape(smstr)[1]
v1 = [1,3,2,3,4,3]
v2 = [1,3,4,3,2,3]
print(hamming_dist2(v1, v2))
|
杰卡德相似系数/杰卡德距离
当数据集为二元变量时,我们只有两种状态:0或者1。这个时候以上的计算相似度的方法就无法派上用场,于是我们引出Jaccard系数,这是一个能够表示两个数据集都是二元变量(也可以多元)的相似度的指标
杰卡德相似系数表示为
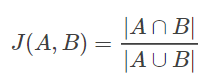
即两个样本的特征集合A和B的交集元素在A和B的并集中所占的比例。杰卡德相似系数越大,两个样本的相似性越大。
杰卡德距离(Jaccard Distance) 是用来衡量两个集合差异性的一种指标,它是杰卡德相似系数的补集,被定义为1减去Jaccard相似系数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| def jaccard_sim(p, q):
'''
计算两个向量的杰卡德相似系数
INPUT -> 长度一致的向量1、向量2
'''
set_p = set(p)
set_q = set(q)
sim = float(len(set_p & set_q))/ len(set_p | set_q)
return sim
def jaccard_dist(p, q):
'''
计算两个向量的杰卡德距离
INPUT -> 长度一致的向量1、向量2
'''
set_p = set(p)
set_q = set(q)
dis = float(len((set_p | set_q)-(set_p & set_q)))/ len(set_p | set_q)
return dis
v1 = [1,3,2,3,4,3]
v2 = [1,3,9,3,4,3]
print(jaccard_sim(v1, v2))
print(jaccard_dist(v1, v2))
|
余弦夹角相似度/余弦距离
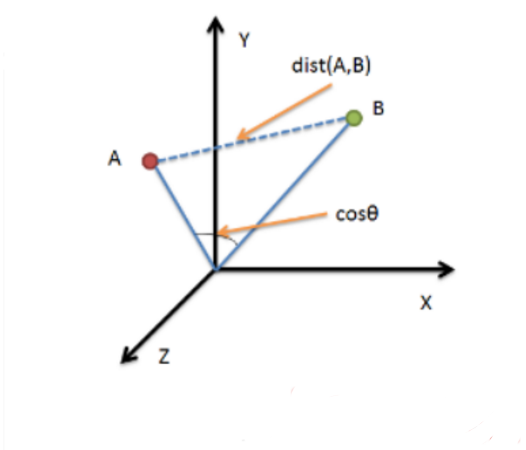
余弦距离,也称为余弦相似度,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1。
1
2
3
4
5
6
7
8
9
10
11
12
| import numpy as np
def cosin_dist(p, q):
'''
计算两个向量的余弦距离
INPUT -> 长度一致的向量1、向量2
'''
return 1-np.dot(p,q)/(np.linalg.norm(p)*(np.linalg.norm(q)))
v1 = [1,3,2,3,4,3]
v2 = [1,3,9,3,4,3]
print(cosin_dist(v1, v2))
|