图的基本概念

图是一种非常神奇的表示方式，生活中绝大多数的现象或情境都能用图来表示，例如人际关系网、道路交通网、信息互联网等等。正如马哲介绍事物具有普遍联系性，而图正好能捕捉这种联系，所以用它来描述这个世界是再好不过的方法。

一、图的定义

1、什么是图

图(G)是一种由”顶点”(Vertex)组成的抽象网络，网络中的各顶点可以通过”边”(edge)实现彼此的连接，表示两顶点有关联。可用数学语言将图(G)描述为一个偶对(V,E)，记为G=(V,E)。其中，V是顶点的集合，E是边的集合。

2、顶点(vertex)和边(edge)

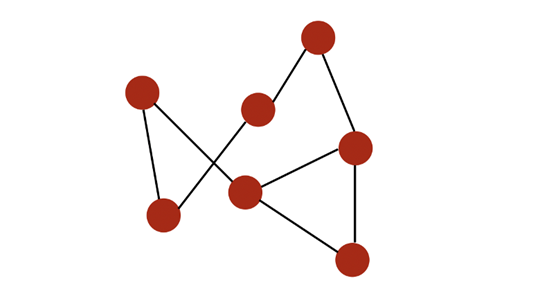
由”图”的定义可以得到最基础最重要的两个概念——“顶点”和”边”。
顶点(vertex)又被称为点、节点、结点、端点，表示某个事物或对象。顶点连接的边数叫做这个顶点的度(dgree)。
边(edge)是顶点之间的连接，表示事物与事物之间的关系。

二、图的分类

1、连通图与非连通图

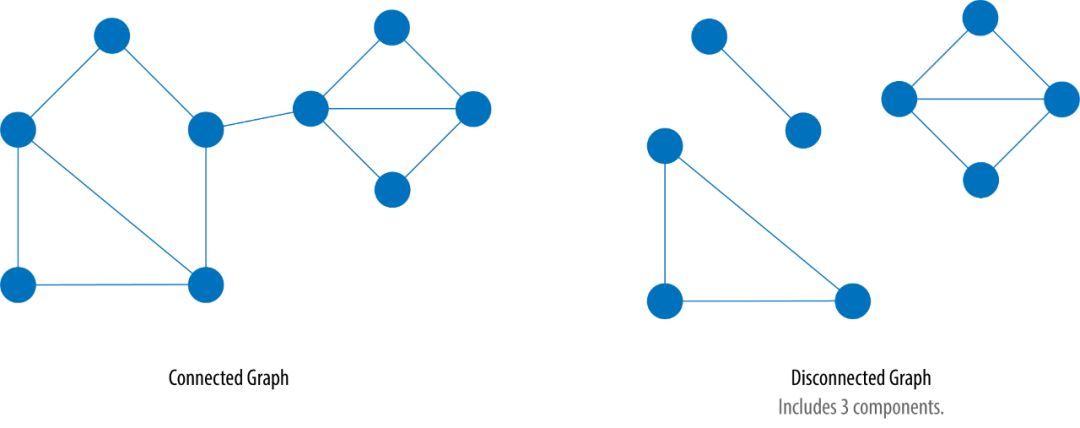
连通图(Connected Graphs)指图内任意两个节点间，总能找到一条路径连接它们，否则，为非连通图(Disconnected Graphs)。也就是说，如果图中包含岛(Island)就是非连通图。

2、未加权图与加权图

未加权图(Unweighted Graphs)的节点和边上均没有权重。对于加权图(Weighted Graphs)，所加权重可以代表：成本、时间、距离、容量、甚至是指定域的优先级。带有权值的连通无向图被称为”网络”。

3、无向图与有向图

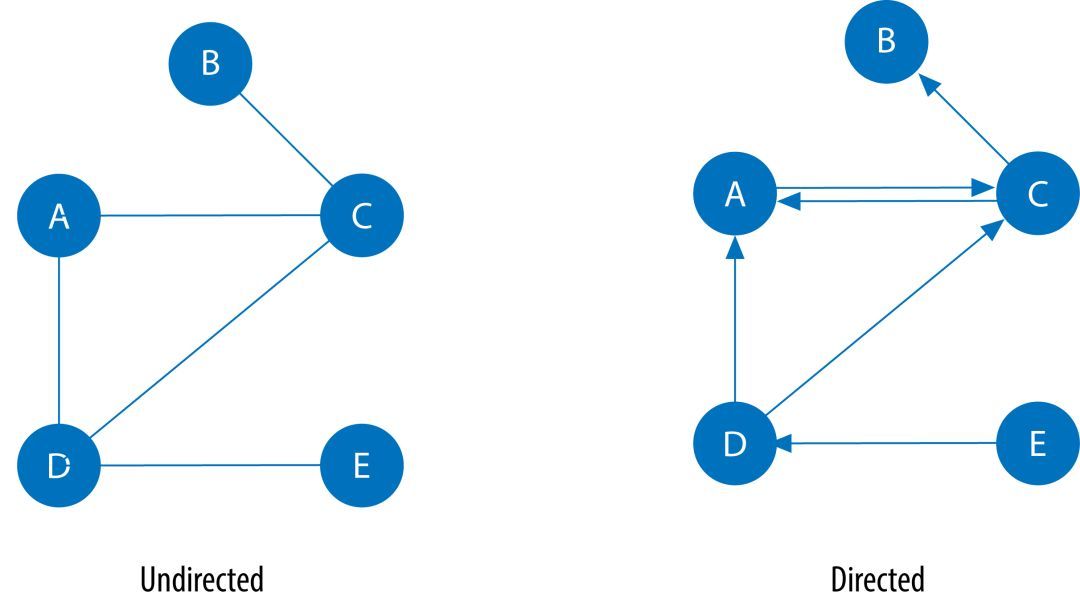
在无向图(Undirected Graphs)中，节点的关系被认为是双向的(bi-directional)，例如朋友关系。而在有向图(Directed Graphs)中，节点的关系可以指定方向。边如果指向了一个节点，我们称为 入边(in-link)，边如果从一个节点出发，我们称为出边(out-link)。
边的方向加入了更多维度的信息。同样关系的边，不同的方向代表了不同的语义信息。下方用有向图绘制了一个简单的社交网络，边的方向代表着”喜欢”。那么从图中我们可以知道，这些人种”最受欢迎的”的是”A”和”C”。

4、循环图与非循环图

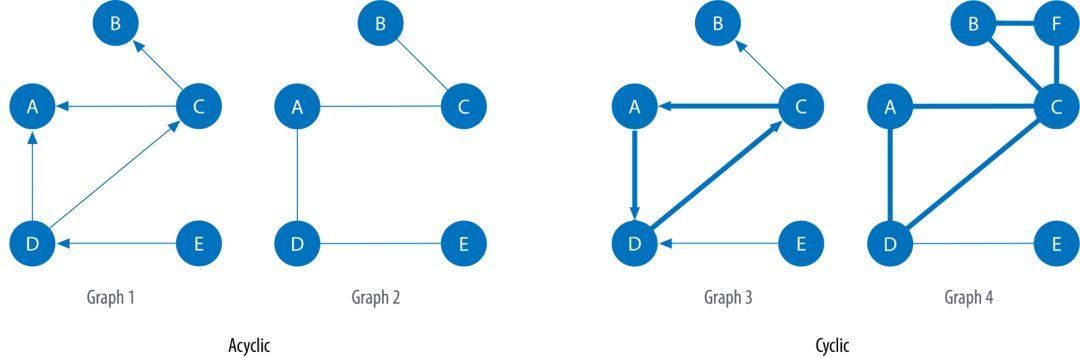
循环指一些特殊的路径，它们的起点和终点是同一个节点。在非循环图(Acyclic Graph)中，不存在循环路径，相反则为循环图(Cyclic Graphs)。有向图和无向图都可能包含循环，所不同的是，有向图的路径必须遵循边的方向。

三、图的存储

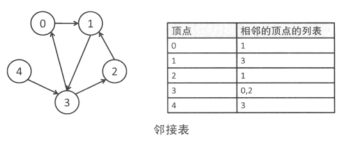
最常用的是邻接矩阵和邻接表。稠密图一般用邻接矩阵，稀疏图一般用邻接表。

1、邻接矩阵法

将每个节点可能的邻居位置排成一行(也就是一个数组，用于对应图中每一个节点)，然后用某种值(如True或False)来表示相关节点是否为当前节点的邻居。

2、邻接表法

邻接表的思想就是存边的信息，而不是点的信息。