监督学习之树模型（1）

决策树算法在机器学习中算是很经典的一个算法系列了，被认为是监督学习方法中最好的并且是最常用的方法之一，特别适合作为集成学习的基学习器。
我们可以将决策树看作是if- then规则的集合，使用决策树模型进行预测的过程就相当于对if - then规则进行判断，那我们可以想到如果if -then规则越多，也就是决策树越复杂，那么预测所需要的时间越长，所以为了不断优化决策树的决策过程，我们需要合理的构建决策树，那么如何来选择if - then的决策规则至关重要。

一、基本概念

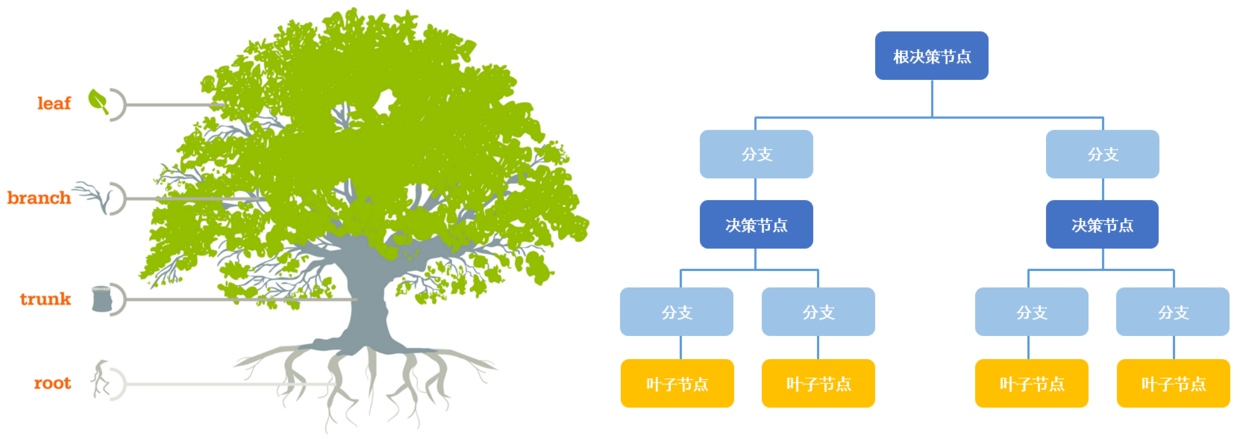
1、节点

（1）按照位置来分：

• 根节点
  它标识整个样本，会被进一步分割成两个或多个子集合。
• 决策节点
  当一个子节点进一步分裂成子节点的时候，它被称为决策节点。
• 叶子/终端节点
  不会被分割的节点被称为叶子或终端节点。

（2）按照关系来分：

• 父节点
  决策节点被子节点称为父节点。
• 子节点
  子节点是父节点的孩子节点。

2、分裂与剪枝

（1）分枝
将一个节点分割为两个或多个子节点的过程。
（2）剪枝
当我们移除掉父节点的子节点时，这个过程成为剪枝。他是分枝的反过程。

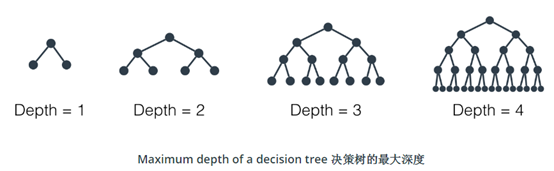
3、最大深度

决策树的最大深度指树根和叶子之间的最大距离。当决策树的最大深度为 k 时，它最多可以拥有 2^k^ 片叶子。

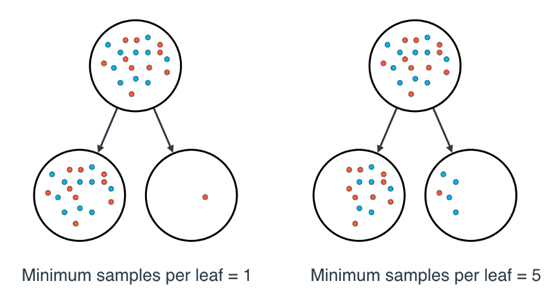
4、每片叶子的最小样本数

在分裂节点时，很有可能一片叶子上有 99 个样本，而另一片叶子上只有 1 个样本。这将使我们陷入困境，并造成资源和时间的浪费。如果想避免这种问题，我们可以设置每片叶子允许的最小样本数。

这个数字可以被指定为一个整数，也可以是一个浮点数。如果它是整数，它将表示这片叶子上的最小样本数。如果它是个浮点数，它将被视作每片叶子上的最小样本比例。比如，0.1 或 10% 表示如果一片叶子上的样本数量小于该节点中样本数量的 10%，这种分裂将不被允许。

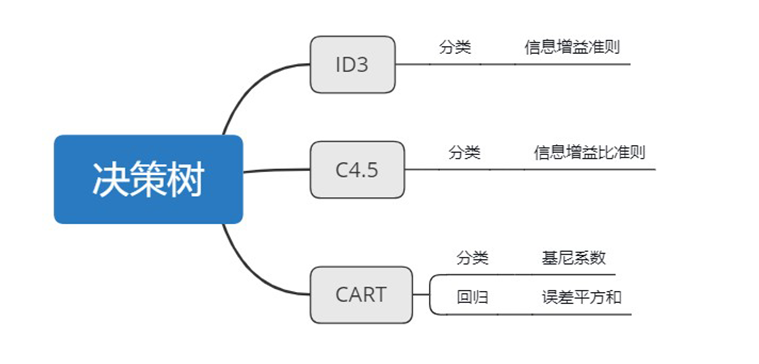
二、常见的决策树算法